
1. 글을 시작하며
안녕하세요. 글 쓰는 아빠 도도한 쭌냥이입니다.
설계 업무를 수행하다 보면 데이터를 분석해서 결과를 예측해야 하는 경우가 많습니다. 이때 다수의 데이터들의 평균값을 이용하게 됩니다. 그래서 오늘은 평균과 관련된 다양한 공식들을 알아보고자 합니다. 아래 참고하시기 바라며, 업무를 하시는 데 있어 도움이 되었으면 합니다. ^^
2. 산술평균(Arithmetic Mean)
모든 데이터 값을 합한 후 데이터의 개수로 나눈 값입니다. 가장 일반적으로 사용되는 평균입니다.
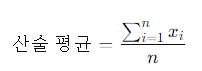
[예시]
데이터 집합 [2, 4, 6, 8, 10]의 산술 평균은 (2 + 4 + 6 + 8 + 10) / 5 = 6
3. 가중평균(Weighted Mean)
각 데이터 값에 가중치 𝑤𝑖를 곱한 후 합계를 전체 가중치의 합으로 나눈 값입니다. 데이터마다 중요도가 다를 때 사용됩니다.

[예시]
과목별 성적에서 각 과목의 배점을 고려한 평균 계산
4. 기하평균(Geometric Mean)
모든 데이터 값을 곱한 후 n제곱근을 취한 값입니다. 비율이나 성장률 계산 시 유용합니다.

[예시]
데이터 집합 [1, 3, 9]의 기하 평균은 (1×3×9)1/3 = 3
5. 조화평균(Harmonic Mean)
데이터 값들의 역수의 산술 평균의 역수입니다. 속도나 비율 계산 시 유용합니다.

[예시]
두 개의 속도 60 km/h와 40 km/h의 조화 평균은 2÷(1÷60+1÷40) = 48 km/h
6. 제곱평균(Quadratic Mean 또는 Root Mean Square, RMS)
각 데이터의 제곱을 평균 낸 후 제곱근을 취한 값입니다. 주로 물리학이나 공학에서 사용됩니다.

7. 중앙값(Median)
데이터 집합을 크기 순으로 정렬했을 때 중앙에 위치한 값입니다. 데이터가 비대칭일 때 유용합니다. 데이터를 순서대로 정렬 후 중앙 위치의 값을 선택하여 중앙값을 결정하면 됩니다.
[예시]
데이터 집합 [3, 1, 4, 2, 5]의 중앙값은 정렬 후 [1, 2, 3, 4, 5]에서 3
8. 최빈값(Mode)
데이터 집합에서 가장 많이 등장하는 값입니다. 데이터의 빈도를 파악할 때 유용합니다. 가장 빈번하게 나타나는 값을 선택하면 됩니다.
[예시]
데이터 집합 [1, 2, 2, 3, 4]의 최빈값은 2
9. 기댓값(Expected Value)
확률 변수의 평균값으로, 각 값에 그 값이 발생할 확률을 곱한 후 합산한 값입니다. 확률과 통계에서 사용됩니다.

[예시]
동전 던지기에서 앞면이 나올 확률이 0.5일 때, 앞면을 1, 뒷면을 0으로 설정하면 기댓값은 1×0.5+0×0.5=0.5
10. 글을 마치며
평균과 관련된 공식은 데이터가 가진 특성과 분석 목적에 따라 적절한 공식을 선택하여 사용하시면 됩니다. 공학 이외에도 다양한 분야에서 응용될 수 있으니 숙지만 하셔도 많은 도움이 되시리라 생각됩니다. 이상으로 글을 마치도록 하겠습니다. 끝까지 읽어주셔서 감사합니다. ^^
'다시 시작하는 공부' 카테고리의 다른 글
| 기본 물리 상수들에 대해서 알아보았습니다. (0) | 2024.10.28 |
|---|---|
| 기술사 응시자격진단 방법 및 조건을 알아보았습니다. (1) | 2024.10.19 |
| 통계학 기초 공식을 알아보았습니다. (0) | 2024.10.11 |
| 동역학 기본 공식을 정리해 보았습니다. (3) | 2024.10.06 |
| 재료역학(고체역학) 기본 공식 (0) | 2024.10.01 |


댓글