반응형

1. 글을 시작하며
안녕하세요. 글 쓰는 아빠 도도한 쭌냥이입니다.
설계 업무를 수행하다 보면 통계학 관련 공식이 필요할 때가 있습니다. 오늘은 통계학 기초 공식들을 알아보려고 합니다. ^^
2. 통계학 기초 공식
2.1 산술평균 (Arithmetic Mean)
데이터 집합의 평균을 구하는 가장 기본적인 방법입니다.
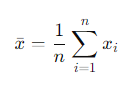
- x̄ : 산술평균
- 𝑛 : 데이터의 개수
- 𝑥𝑖 : 각 데이터 값
2.2 중앙값 (Median)
데이터를 크기 순으로 배열했을 때 중앙에 위치한 값입니다.
- 데이터의 개수가 홀수일 때: 중간 위치의 값
- 데이터의 개수가 짝수일 때: 중앙에 위치한 두 값의 평균
2.3 최빈값 (Mode)
데이터 집합에서 가장 자주 나타나는 값입니다.
2.4 분산 (Variance)
데이터가 평균으로부터 얼마나 흩어져 있는지를 나타내는 척도입니다.
모집단 분산(𝜎2)
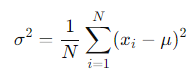
표본 분산(𝑠2)
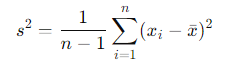
- 𝜇 : 모집단 평균
- x̄ : 표본 평균
- 𝑁 : 모집단의 크기
- 𝑛 : 표본의 크기
2.5 표준편차 (Standard Deviation)
분산의 제곱근으로, 데이터의 흩어짐 정도를 원래 단위로 표현합니다.

2.6 표준오차 (Standard Error)
표본 평균의 표준편차로, 모집단 평균 추정의 정확도를 나타냅니다.
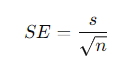
- 𝑠 : 표본 표준편차
- 𝑛 : 표본의 크기
2.7 신뢰구간 (Confidence Interval)
모집단 평균에 대한 추정 범위를 나타냅니다.
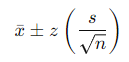
- 𝑧 : 신뢰 수준에 따른 z-값 (예: 95% 신뢰 수준일 때 𝑧 ≈ 1.96)
- 𝑠 : 표본 표준편차
- 𝑛 : 표본의 크기
2.8 확률 밀도 함수 (Probability Density Function, PDF)
연속 확률 변수의 분포를 나타내는 함수입니다. 예를 들어, 정규분포의 PDF는 다음과 같습니다.
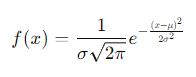
- 𝜇 : 평균
- 𝜎 : 표준편차
2.9 이항 분포 (Binomial Distribution)
성공 확률이 𝑝 p인 실험을 𝑛 n번 수행했을 때, 정확히 𝑘 k번 성공할 확률.
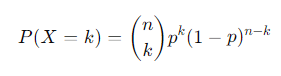
- nCk : 조합
- 𝑝 : 성공 확률
- 𝑘 : 성공 횟수
2.10 회귀분석 (Regression Analysis)
독립 변수와 종속 변수 간의 관계를 모델링합니다.
단순 선형 회귀의 경우:
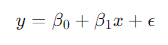
- 𝑦 : 종속 변수
- 𝑥 : 독립 변수
- 𝛽0 : y-절편
- 𝛽1 : 기울기
- 𝜖 : 오차항
3. 글을 마치며
이상으로 통계학 기초 공식 10가지를 알아보았습니다. 다음에는 평균의 종류를 알아보도록 하겠습니다. 기사 공부나 설계 업무 시 도움이 되었으면 합니다. 끝까지 읽어주셔서 감사합니다.
728x90
반응형
'다시 시작하는 공부' 카테고리의 다른 글
| 기술사 응시자격진단 방법 및 조건을 알아보았습니다. (1) | 2024.10.19 |
|---|---|
| 평균과 관련된 공식을 알아보았습니다. (산술평균, 가중평균, 기하평균, 조화평균, 제곱평균 등) (2) | 2024.10.15 |
| 동역학 기본 공식을 정리해 보았습니다. (3) | 2024.10.06 |
| 재료역학(고체역학) 기본 공식 (0) | 2024.10.01 |
| 스테인레스 304, 316, 430 재질(소재)에 대해서 알아보았습니다. (1) | 2024.09.29 |


댓글